Définition
Équation diophantienne : équation polynomiale à une ou plusieurs inconnues dont les coefficients et les solutions sont entiers
(
Fonction polynômiale,
Polynôme,
Racine)
Résolution
Proposition :
Considérons l'équation $$ax+by=c$$ où \(a,b,c\in{\Bbb Z}\)- L'équation possède des solutions \((x,y)\in{\Bbb Z}^2\) si et seulement si \(\operatorname{pgcd}(a,b)|c\)
- Si \(\operatorname{pgcd}(a,b)|c\), alors il existe même une infinité de solutions entières et elles sont exactement les \((x,y)=(x_0+\alpha k,y_0+\beta k)\) avec \(x_0,y_0,\alpha,\beta\in{\Bbb Z}\) fixés et \(k\) parcourant \({\Bbb Z}\)
(
Identité de Bézout,
Pgcd,
Division - Diviseur - Divisibilité)
Théorème de WilsonDernier théorème de Fermat - Grand théorème de Fermat - Théorème de Fermat-Wiles
Exemples de résolution
Résoudre \(ax+by=c\) : ^[
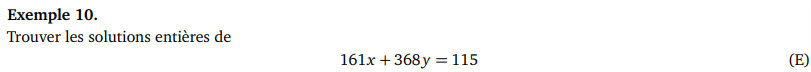
]